Number System

Types of Numbers Systems:

Venn diagram of Real number System

• Natural Numbers (N): 1, 2, 3, 4, and so on ...

  

  Useful to count number of items.

• Whole Numbers (W) : 0 and (N) : 0, 1, 2, 3, 4, and so on ...

  

  In whole numbers, 0 is also considered along with all Natural numbers

  
  

• Integers (Z) : (W) and -ve of (N) : ... and so on -4, -3, -2, -1, 0, 1, 2, 3, 4, and so on...

Positive Integers indicates Profits and Negative Integers indicates Loss

• Rational Numbers (Q) : number that can be written in p/q form, where q ≠0. Example: 1/3, 14/16, and so on...

  

  A thing divided into equal parts.

• Irrational Numbers (S) : number that cannot be written in p/q form, where q ≠0. : Example: √2, √3 and so on...

Accurate Distance in geometry needs use of irrational numbers

• Real Numbers (R) : (Q) and (S)

  

Important Terms:

Co-prime numbers, also known as relatively prime or mutually prime numbers, are two or more integers that have no common factors other than 1. Example : 8/15, 4/15 and so on...

Equivalent rational numbers are different ways of representing the same value. Example 2/5=4/20=8/40 and so on... or 4/6 = 8/12 = 16/24 and so on...

Terminating fractions are those rational numbers whose decimal expansion terminates or ends after a finite number of steps. Example 7/8=0.875 or 1/2=0.5 or 639/250=2.556 and so on...

Non-Terminating recurring (repeating) fractions are those rational numbers whose decimal expansion do not terminates or ends after a finite number of steps. Example 1/3=0.333...= 0.‾3‾ or 1/7=0.142857142857142857...=0.‾142857‾ and so on.... These decimal expansion are written with the bar above the digits, indicating the block of digits that repeats.

Non-Terminating non-recurring (non-repeating) fractions are all irrational numbers whose decimal expansion do not terminates or ends after a finite number of steps and the sequence of numbers do not repeat even after many number of steps. Example √2=1.414213562...  or √3=1.732050807... and so on....

Fundamentals :

Irrational numbers also satisfy the commutative, associative and distributive laws for addition and multiplication. However, the sum, difference, quotients and products of irrational numbers are not always irrational.

useful to solve various operations on irrational numbers

useful to solve various power and exponents problems

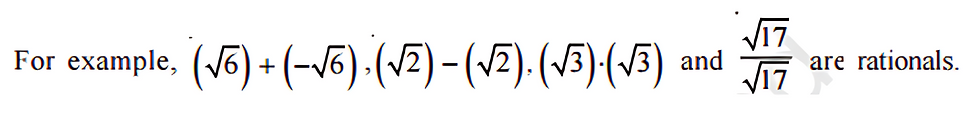
Techniques / Type of Questions:

• True or False with reason.

  1. Every whole number is a natural number. False, because zero is a whole number but not a natural number.

  2. Every integer is a rational number. True, because every integer m can be expressed in the form m/1, and so it is a rational number.

  3. Every rational number is an integer. False, because 3/5 is not an integer.

• Find some rational or irrational numbers between two numbers.

  • Find five rational numbers between 1 and 2.

    Since we want five numbers, we write 1 and 2 as rational numbers with denominator 5 + 1 i.e., 1 = 6/6 and 2 = 12/6.

    So, the five numbers are 7/6, 8/6, 9/6, 10/6 and 11/6.

    7/6 and 11/6 cannot be further reduced as 7 and 6 are co-prime numbers.

    But, 8/6 can be further be reduced to 4/3; 9/6 can be reduced to 3/2; 10/6 can be reduced to 5/3.

    So, final answer could be 7/6, 4/3, 3/2, 5/3 and 11/6.

  • Find five irrational numbers between 1 and 2.

    Since we know irrational numbers are neither repeating nor terminating in decimal form, five irrational numbers between 1 and 2 can be:

    1.1021..., 1.102101..., 1.102101002..., 1.1021010020003..., and 1.102101002000300004....

    These numbers continue infinitely without repeating.

    The three dots (...) indicate that the number is non-terminating, which is a necessary condition for a number to be irrational in decimal form.

• Locate √x, where x = Natural number on number line. Example: locate √3 on number line.

Pythagoras Theorem with 1 unit x 1 unit gives √2. Here OA = AB = 1 unit gives OB = √2. with one more triangle side of 1 unit, BD, will give √3, OD.

• Locate √x, where x = Positive decimal number on number line. Example: locate √3.5 on number line.

  

  Take x + 1 units, here 3.5+1 cm, as diameter of the semicircle. Locate AB as x units (here 3.5 cm). Draw Perpendicular from B to the Semicircle. BD = √x

Click to view the video

• Find the decimal expansions of a fraction.

  For Example decimal fraction of 10/3, 7/8 and 1/7

  

  Fraction Form to Decimal Form by carrying out simple division of Numerator by Denominator

• Find the Rational number (p/q) expansions of a decimal number.

  For Example find rational number of 0.875 , and 0.3333...

  

• Addition , Subtraction , Multiplication and Division of Irrational Numbers

  For example

  

• Rationalize the denominator of irrational number.

  

Tip: Use these properties to Solve Irrational Numbers

• Simplify irrational numbers with base and exponent

  Example:

  

Tip: Use these properties to Solve Irrational Numbers